We have seen in Part 1 and Part 2 that neural architecture search can be used to find hyperparameters and to design recurrent networks. Is there any more use to it? The answer is obviously yes (otherwise there would be no point on this post). Let’s recap, NAS is just a method where you learn something that is non-learnable by backpropagation using trial and error, aka, reinforcement learning. The key for using it in more complex settings is to have a well defined space of parameters. In the first part that space was simply the real range for each hyperparameter. In the second part the search space included every recurrent network. Since that is a pretty broad space we narrowed it down by only working with some specific recurrent networks that could be generated by a tree-like structure. In this third part the search space is going to be the set of all convolutional neural networks. And to reduce that space to something manageable we are only going to consider networks generated by residual connections. Residual connections are typically just an addition operation like this

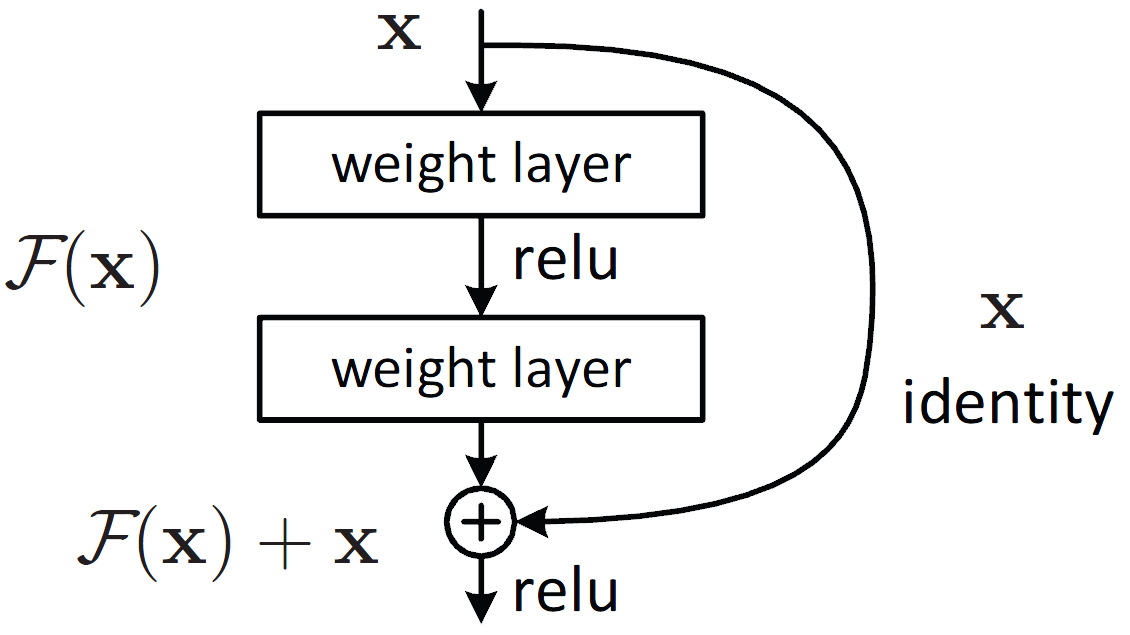
The good property of residual connections is that they prevent vanishing gradients for very deep networks. Their discovery allowed to increase the number of layers. ResNet achieved state of the art results when it was first created, and big transformer-based architecture also use residual connections. Normally the residual connection is between one layer and the next one. Can you think of a way of generalising this? Is there a ways of creating a bigger set of possible architectures? Similar to what we did for recurrent networks, we could break that restriction of just connecting to the next layer. This way we could end up with something like the architecture presented in the original NAS paper

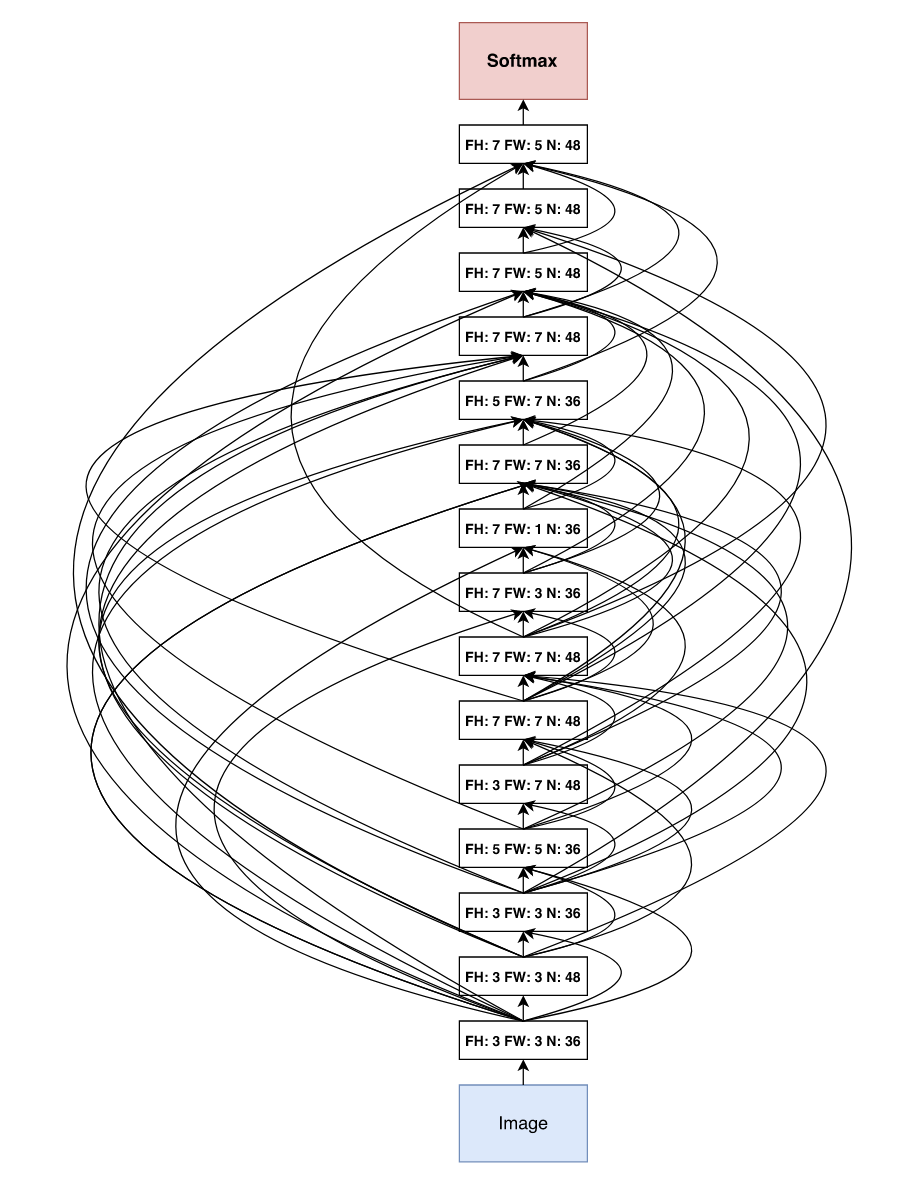
Again, the real question is how to encode that architecture, because using a picture is not quite computer-friendly. Think of the way of representing a graph, you use the adjacency matrix, or the adjacency lists. Here it is similar, for each layer you just need to know the inputs. Or in other words, the architecture is saved as adjacency lists of incoming vertices. That’s simple enough for the controller to generate. For each layer the controller has an array of previous layers and simply selects one or more indices from there representing the incoming residual connections. The rest of hyperparameters are generated afterwards. See the diagram

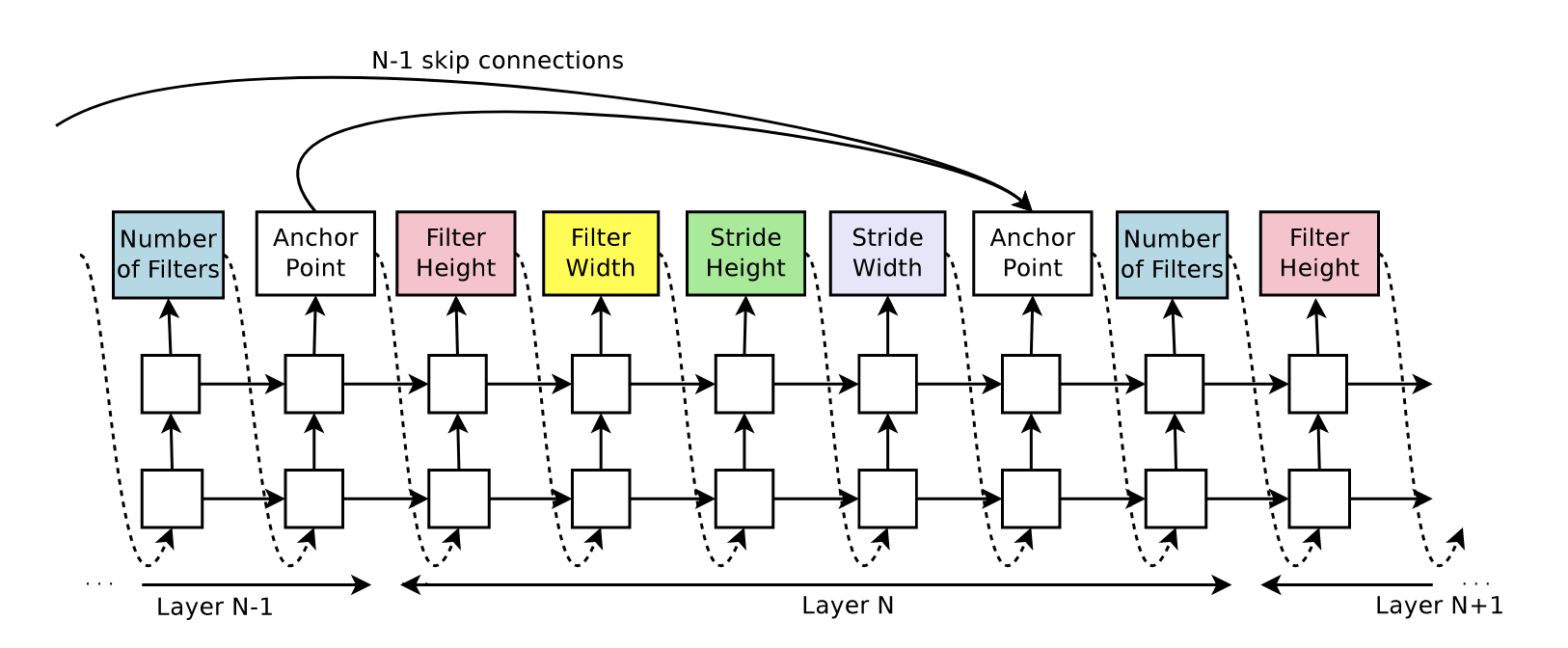
What the anchor point box is doing is just that, sampling indices representing the incoming layers. That box may implemented as a feed forward network with several classes. It could seem that the number of classes varies and so we cannot fix the last layer to have a constant size, and that is true, but for a given layer it is always the same. Therefore, fixing the total number of layers also fixes the number of output classes for each anchor point and so we can train them. Another reasonable way to implement the anchor box is as a multinomial variable. That way you only need to learn the probabilities, maybe conditioned to something. Although that poses another problem since another way of applying backpropagation needs to be designed, probably by using some reparameterisation trick. The original implementation was done through attention. They gave some hidden state to each anchor box and used Bahdanau attention mechanism to select the most similar layers (according to that hidden state that is learnable) to use as residual connections. This solves the problem of variable sized input, you can use the same attention mechanism for every anchor point. Thus, reducing the number of total parameters while making all the connections related to each other.

But simply selecting residual connections at random has one issue, have you seen it? There could be layers without connections, or layers that are not connected to anything. The solution is simple, for those layers that are not connected, you simply connect them to the last layer. And for those that doesn’t receive any input, the input image is used as the input, and not any other layer. This way, many complex architectures can emerge, not just linear ones. And there you have it, you can use reinforcement learning to explore the search space of convolutional neural networks.

Here I have presented you three ways of using neural architecture search to better design neural network architectures. If you are feeling short of ideas to create networks, maybe try designing a broad search space and traing a NAS controller on a toy dataset. And don’t feel that it is an outdated technique, Google is still using it, see this article. The main disadvantage of this tecnique is that it requires a lot of computational power, but as everything else, you can use it with reduced capabilities on smaller datasets to try on your own. Maybe you find the next transformer this way, who knows?