Uno de enero, todo el mundo se propone cambiar algún hábito. Pocos los consiguen. En mi caso no me propuse nada pero surgió una idea que posteriormente se transformó en costumbre. Ese mismo día le pregunté a un amigo mío que me recomendara un libro para leer. Llevo años sin leer en serio y como no sabía por dónde empezar dejé que esa decisión la tomaran por mi. La recomendación fue “Momentos estelares de la humanidad” de Stefan Zweig. Tardé más de un mes en comprarlo y otro mes en leerlo. Cuando acabé llegué a la conclusión de que no era de mi estilo. No obstante, volví a probar suerte. La siguiente recomendación fue “El señor de las moscas” de William Golding. Este sí fue de mi agrado. Y a partir de ahí, surgió un hábito. Este año estoy viajando a través de los gustos literarios de mis amigos y amigas. Libro tras libro. Leer el libro favorito de alguien te revela mucho sobre su forma de ser. Y también te abre la mente a lecturas que de normal rechazarías. Requiere disciplina. De momento llevo 9 ejemplares añadidos a mi colección siendo el último del que vengo a hablar hoy.

El libro titulado “Pensar rápido, pensar despacio” fue escrito por Daniel Kahneman, un psicólogo con un premio Nobel de economía. El autor reúne en esas 672 páginas toda su carrera profesional. Es una colección extensa de experimentos obtenida tras varias décadas de trabajo. Un libro de ensayo que expone una tesis de una forma muy similar a como Susan Cain expresaba la suya en “El poder de los introvertidos”. Varios experimentos me he encontrado que se hallaban en ambos libros. Sin embargo, cada autor los ve con sus propias gafas. Yo también he sacado mis propias conclusiones, pero creo que es más interesante exponer los experimentos desprovistos de connotaciones y que cada cual aprenda lo que quiera de ellos. Además de los experimentos también explicaré algunos conceptos que trata el libro y añadiré algunos detalles que me parecen relevantes.

Antes de seguir, vea el siguiente vídeo a pantalla completa:

¿Vió al gorila? La mitad de las personas no lo ven. Cuando focalizas tu atención en una tarea, olvidas las demás. Ese era el primer experimento llamativo del libro. Casi todos los experimentos tienen un efecto similar. Inicialmente nada parece sorprender. Todo es intuitivo y obvio. Pero cuando te explican el trasfondo te das cuenta de lo sesgada que es la percepción humana, hasta el punto de no ver un gorila enorme. Posiblemente algunos de ustedes sí que vieran el gorila. Esto no es una ciencia natural, es una ciencia social. Por eso cada experimento se debe hacer con una muestra poblacional representativa. En este caso Christopher Cabris y Daniel Simons lo probaron con personas de distintas edades, culturas, educación y género. La conclusión es que el efecto es inequívocamente válido para toda la población mundial. La mitad de las personas no ven al gorila y la otra mitad sí. Parece imposible no verlo, ¿verdad? Pues igual de sorprendentes son muchos de los experimentos y resultados que expondré a continuación.

Heurística de la disponibilidad

Propóngase usted dar 20 ejemplos de situaciones en las que se mostró con un carácter firme frente a la adversidad en el que demostraba su capacidad ejecutiva.

¿Ya? ¿Se siente más o menos seguro de sí mismo? En eso consistía este otro experimento. Muchas de las personas entrevistadas se sentían menos seguras si se les había pedido muchos ejemplos y en cambio, las que se les preguntó menos ejemplos se sentían más seguras. Un curioso resultado. Si doy más ejemplos de seguridad me siento menos seguro. A este efecto también se le conoce como sesgo de disponibilidad. La inseguridad viene de que los últimos ejemplos cuestan más de recordar que los primeros. Cuando nos cuesta encontrar argumentos nuestro cerebro genera dudas sobre esa postura. Este efecto se puede eliminar si a esa dificultad cognitiva se le da una explicación, como por ejemplo decirle a los participantes del estudio que les va a costar más encontrar ejemplos por el ruido de la clase de al lado.

Efecto de mera exposición

Zajonc decidió publicar palabras inventadas en el periódico durante varias semanas. Después, al preguntarle a las personas qué palabras les gustaban más, las que habían visto en el periódico recibieron mayor puntuación. Todo ello a pesar de que son palabras sin significado ninguno.

Igual de llamativo es este otro resultado en el que Todorov conseguía predecir el resultado de las elecciones basándose en las puntuaciones que los participantes del estudio daban a las caras de los políticos. Es remarcable porque los participantes evaluaban la competencia de la persona basándose solo en la cara y siendo estas caras de políticos de países arbitrarios sin relación alguna con los participantes. Es como si Tezanos se va a Australia y hace encuestas solo enseñando las caras de los políticos españoles a los australianos. Posiblemente acertaría más.

Y en la misma línea hay otro artículo que muestra cómo los políticos guapos que aparecen más en televisión obtienen mejores resultados, simplemente por aparecer más en televisión. La mera exposición los hace recibir una mayor aprobación.

Efecto halo

El autor describe el concepto de efecto halo como el hecho de asociar a una persona solo atributos positivos o solo atributos negativos. O como los autores también lo describen: “What You See Is All There Is”. Evaluamos el todo por una parte. Prueba de ello quedó reflejado en el estudio de Solomon Asch. En él se preguntaba la opinión de dos personas:

1
2
3
Alan: inteligente-diligente-impulsivo-crítico-testarudo-envidioso

Ben: envidioso-testarudo-crítico-impulsivo-diligente-inteligente

Seguramente te hayas percatado de que son la misma descripción. Pero recibieron valoraciones dispares, obteniendo Alan puntuaciones más favorables que Ben. Los adjetivos del principio terminan acaparando la atención y cogen más peso que los del final. Ese es el efecto halo. Básicamente es formarse un prejuicio e ignorar la información que lo contradiga. También hay que notar que si se evalúan por separado o conjuntamente la visión cambia. Cuando evalúas los dos perfiles conjuntamente es más fácil darse cuenta de su equivalencia. Esta diferencia entre evaluar conjuntamente y por separado quedó plasmada por Christopher Hsee. En su experimento preguntó a varias personas que evaluaran dos vajillas. Una tenía 24 unidades en perfecto estado y otra tenía 40 unidades con 9 de ellas rotas. Cuando veían las dos conjuntamente se valuaban a un mayor precio la de 40 porque era exactamente igual que la de 24 pero con más piezas. Sin embargo, cuando se valoraban por separado la de 40 acababa recibiendo un menor precio debido al hecho de contener platos rotos. Un efecto que Hsee denominó como “menos es más”. El propio Kahneman realizó un experimento similar. En este caso menos es más hace referencia a probabilidades. Es una proposición matemática el que la probabilidad de la intersección de dos eventos es igual o menor que la de cada evento por separado. En lenguaje llano esto nos viene a decir que es más probable encontrar un gato en la calle que encontrar un gato en la calle que a la vez sea blanco. Cada propiedad adicional reduce la probabilidad de que suceda. Pero a ojos de la gente esto no siempre es así. El experimento comenzaba describiendo a una mujer:

Linda tiene treinta y un años, es soltera, franca y muy brillante. Se especializó en filosofía. De estudiante le preocupaban mucho los asuntos de discriminación y justicia social, y también participó en manifestaciones antinucleares.

Y posteriormente se pedía evaluar las probabilidades de los siguiente hechos:

• Linda es profesora de primaria.
• Linda trabaja en una librería y recibe clases de yoga.
• Linda milita en el movimiento feminista.
• Linda presta asistencia social en psiquiatría.
• Linda es un miembro de la Liga de Mujeres Votantes.
• Linda es cajera de un banco.
• Linda es corredora de seguros.
• Linda es cajera y activista del movimiento feminista.

De esta lista los eventos de interés son “cajera de banco” y “cajera de banco feminista”. Las personas dieron menor probabilidad a cajera de banco. Sin embargo, toda cajera de banco feminista es a su vez cajera. Luego la probabilidad es estrictamente menor. Menos es más.

Regresión a la media

Esto no es un experimento per se sino más bien un hecho estadístico igualmente remarcable. Considérese la distribución de probabilidad (PDF) de una gaussiana:

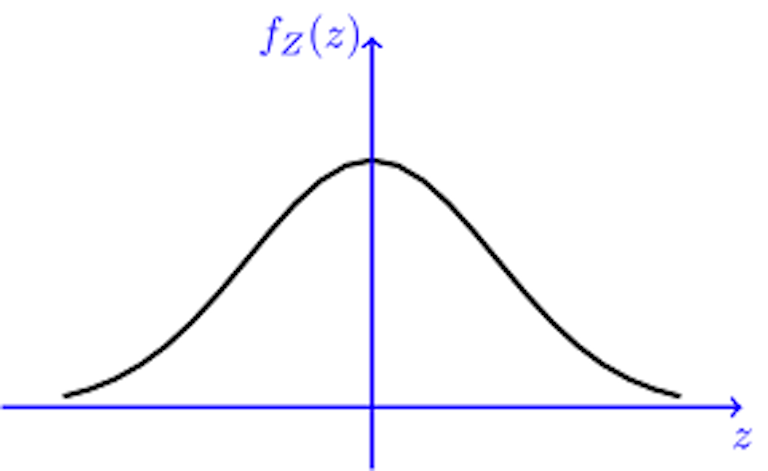
Supongamos que muestreamos a partir de dicha PDF dos veces de forma independiente. Y yo ahora le digo que la primera ha salido con un valor muy a la derecha. ¿Qué es más probable? ¿Que la segunda esté a la izquierda o a la derecha de la primera? Si observamos el siguiente gráfico se ve que claramente es más probable que esté a la izquierda. El área bajo la curva es mayor. La probabilidad de que quede en el área sombreada es superior a un medio como se ve en la función de la derecha.

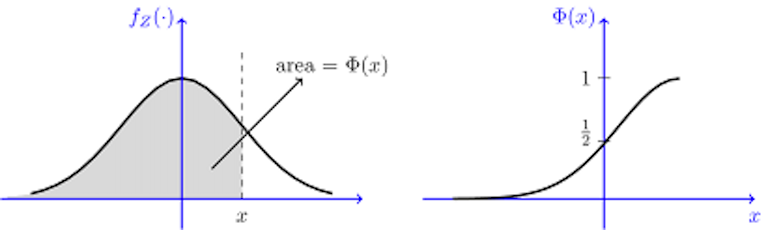
Esto es el efecto de regresión a la media. Un ejemplo más palpable sería la inteligencia de los hijos. Si tus hijos son extraordinariamente avispados, es muy probable que tus nietos lo sean menos. Y al revés también. O en el caso del autor, un soldado que resolvía una prueba de forma excelente solía obtener un peor resultado en la siguiente. Y quién lo hacía muy mal, lo solía hacer mejor después. Esto sucede cuando dos variables se hallan poco correlacionadas, como en los ejemplos anteriormente expuestos.

Fallos médicos

Un análisis sobre errores médicos en la UCI concluyó que “los médicos que creían estar ‘completamente seguros’ de su diagnóstico ante mortem estaban equivocados en el 40 por ciento de los casos”. De forma completamente independiente, en el libro también se relata la historia de un médico del siglo XX que siempre acertaba en sus diagnósticos de tifus pero resultó que era porque tocaba las lenguas de los pacientes sin lavarse causando la propia enfermedad. Posteriormente también se muestra como los psiquiátras evaluaban de forma diferente el riesgo de violencia de un paciente en función de si la información se le presentaba en formato frecuencial o absoluto, es decir, quien leía que hay un 10% de probabilidades de violencia se sentía menos reacio a liberar a un paciente que quien leía que 10 de cada 100 pacientes similares son violentos. En concreto, el 41% denegaron el alta al paciente en el primer caso y el 21% en el segundo caso.

Efecto espectador

Este es posiblemente de los estudios más antiguos del libro. John M. Darley realizó el siguiente experimento un tanto macabro. Había diversos participantes cada uno en una salita aislada con un micrófono en su interior. Cada persona solo podía hablar cuando era su turno. En una de las intervenciones el interlocutor mencionaba su inclinación a sufrir ataques de ansiedad. Poco después, el actor que interpretaba ese papel fingía sufrir uno de esos ataques y pedía ayuda a la vez que parecía ahogarse. En medio de su sufrimiento su micrófono se corta y se da pie al siguiente participante a hablar. ¿Cuántos creéis que pidieron ayuda? De los 15 participantes, 4 pidieron ayuda inmediatamente, seis no salieron de la cabina y cinco salieron algo después de que el micrófono se cortara. Este efecto muestra que cuando hay otras personas alrededor, nos sentimos menos proclives a actuar frente a emergencias.

Ahora ya sabe que una primera estimación de la probabilidad de ayuda es del 27% en casos de emergencia (4 de 15). Dado ese conocimiento, si se le presentasen otros 15 individuos y se le pidiera que identificara quién saldrá a ayudar y quién no, ¿acertaría el porcentaje? Presentado así, lo más lógico seguramente sea predecir de nuevo que solo 4 irán raudos a salvar al afectado. Pero otro estudio mostró que conocer la tasa base no afecta en las predicciones de la población. Incluso aún sabiendo que un evento tiene una determinada probabilidad, si nuestra creencia es contraria a ese hecho, las predicciones se alejarán de esa probabilidad. Algo similar sucede con la inversión en bolsa. El consejo financiero más básico es aguantar tu posición y esperar a que el mercado responda. Históricamente el precio de las acciones ha subido alrededor de un 10%. Es solo cuestión de esperar. Pero muchas personas creen tener información privilegiada del mercado que les permitirá sacar ventaja de las fluctuaciones diarias. Esta ilusión de sagacidad es lo que lleva a que los inversores individuales pierdan sistemáticamente contra las instituciones financieras. Estimándose que un 2.2% del PIB se transfiere de inversores individiduales que realizan una compraventa frecuente hacia las instituciones financieras. De igual manera, también se ha observado que las mujeres son consistemente mejores inversoras que los hombres.

Entornos de poca validez

La ilusión de sagacidad antes presentada en gran parte se debe a intentar predecir algo que es impredecible. En eso consiste un entorno de poca validez. Para poder llegar a ser un experto no es solo suficiente con dedicar 10.000 horas de tu tiempo. También tienes que recibir un feedback consistente y estadísticamente significativo. El azar puede llegar a alterar la percepción de la habilidad. Uno de los ejemplos que se suele exponer es el de los radiólogos. Es una disciplina en la cual el feedback es tardío y en muchos casos no es concluyente al 100%. Esto lleva a que ser experto en radiología sea más difícil que serlo en otras disciplinas donde hay una respuesta inmediata y clara respecto a tus acciones. Similar a radiología es la histopatología. Durante mi colaboración con el Vall d’Hebrón era perceptible la complicación del asunto. Determinar si una célula es o no cancerígena tiene un cierto componente aleatorio. Kahneman explicaba también que determinar la valía de un soldado en pos de un examen psicológico dependía más del azar de lo que le gustaría.

Afortunadamente hay soluciones. Cuando se necesita un determinado juicio de valor es posible conseguir un resultado más objetivo. El autor del libro explicaba que lo que él hizo fue separar la prueba en diversas subpruebas de menor alcance. Cada una mucho más específica que la evaluación general. A su vez, el resultado de cada entrevista se asignaba a un profesional distinto el cual solo daba una puntuación subjetiva de su percepción de ese aspecto. Posteriormente, todas las puntuaciones se combinaban en un único resultado. De esta forma se consigue domar un poco más la intuición. Este sistema de evaluación por tokens también lo desplegó un antiguo profesor mío de literatura para evaluar debates. Fernando Fedriani hizo su tesis doctoral en un sistema de evaluación del debate. De nuevo, mediante la creación de tokens se consigue que el evaluador reduzca sus sesgos a unos atributos concretos. Al promediar los resultados los efectos azarosos quedan reducidos, resultando en un método más objetivo.

En el ámbito médico también es posible dotar a los profesionales de herramientas para conseguir mejores diagnósticos. Sin embargo, como describe el autor del libro, los especialistas son reticentes a aceptar esos cambios. A pesar del cuerpo de evidencia creciente, el statu quo tiene bastante peso.

Pre mortem

Una técnica exitosa para mitigar los efectos de los sesgos humanos es lo que el autor denomina como el pre mortem. Es un ejercicio simple. Considere este escenario. Es un ejecutivo de una empresa que está planeando un proyecto a largo plazo. Ha hecho la investigación pertinente y sabe los riesgos y posibles beneficios. Sin embargo, es posible que haya sobrestimado la posibildad de éxito. Así que la solución es la siguiente. Imagínese que ha pasado un año y el proyecto ha fracasado estrepitosamente, ¿por qué? Intente dar una explicación de qué ha salido mal. Así es como Kahneman descubrió que los ejecutivos conseguían estimar con mayor precisión los verdaderos riesgos así como los plazos necesarios para llevar a cabo sus proyectos.

Ley Weber-Fechner

Esta ley psicofísica es una formulación matemática de la percepción humana a los estímulos. Fechner descubrió que la percepción de un estímulo escala acorde al logaritmo de la magnitud del mismo. De manera parecida sucede en la percepción de la utilidad de dinero. De forma aproximada Kahneman nos muestra el siguiente gráfico:

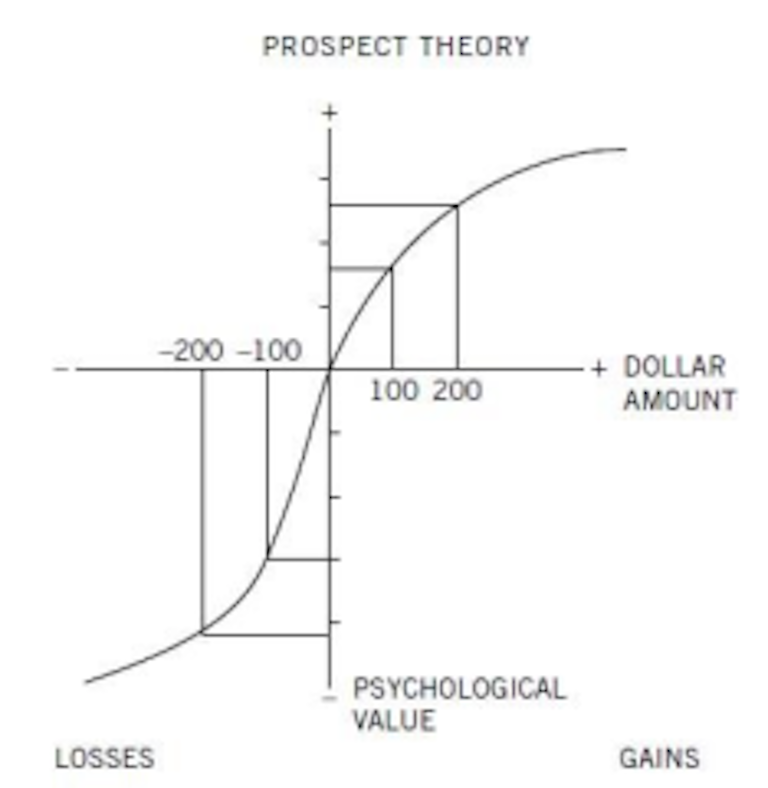
Y nos explica que para quien es rico 200€ valen menos que para quien es pobre. Nada remarcable. De igual manera perder 200€ te duele más si solo tienes 200€ que si tienes 200.000€. Y parece evidente también que perder duele con más fuerza que ganar. Son hipótesis sencillas y bastante aceptables. Pero las conclusiones que se deducen de ellas veremos que no lo son tanto. Primero a través de dos preguntas y luego más rigurosamente con el teorema de Rabin. Empecemos por la primera pregunta, tiene que que escoger entre dos opciones:

• 25% probabilidad de ganar 240€ y 75% probabilidad de perder 760€.
• 25% probabilidad de ganar 250€ y 75% probabilidad de perder 750€.

La segunda opción es claramente mejor y así lo decidieron todos los participantes del estudio. Ahora se presentan otras dos elecciones diferentes. Primero elija entre:

• 100% probabilidad de ganar 240€.
• 25% probabilidad de ganar 1000€ y 75% probabilidad de no ganar nada.

Y luego elija entre:

• 100% probabilidad de perder 750€.
• 75% probabilidad de perder 1000€ y 25% probabilidad de no perder nada.

Si es como la mayoría de participantes del artículo del apéndice B del libro seguramente tenga aversión al riesgo en las ganancias apostando por la cantidad segura e inclinación al riesgo en la pérdidas apostando por la posibilidad de no perder nada. De igual manera en la primera pregunta habrá escogido la opción dos sin dudarlo. Pues ahora viene la contradicción. Si escogió la opción segura de ganar 240€ y la incierta de no perder nada, eso es equivalente a la opción 1 de la primera pregunta que claramente rechazó. Un mismo problema enmarcado de dos formas distintas lleva a decisiones opuestas.

Kahneman trabajó durante mucho tiempo con un compañero llamado Amos. Amos comprobó que este efecto marco se podía usar para manipular las decisiones de los expertos en salud pública. En una conferencia sobre lo que denominaban enfermedad asiática a la mitad de los asistentes se les presentó una versión que ilustraba una posible solución junto con las posible vidas salvadas. A la otra mitad les mostró el programa pero les explicó cuántas personas morirían. En esencia es lo mismo, si de 1000 personas 100 fallecen, eso implica que 900 sobreviven. No cambia en absoluto la eficacia del tratamiento el exponerlo en términos de fallecimientos que de salvaciones. Pero los funcionarios que asistieron sí que tomaron decisiones diferentes en función de la versión escuchada.

Otro caso peculiar es sobre las deducciones fiscales por hijos. Thomas C. Schelling explicaba en su libro Choices and Consequences uno de estos efectos marco. En él presentaba dos escenario que en principio son equivalentes pero no lo parecen. El primer escenario consistía en una posible ley sobre deducciones fiscales por hijos. La pregunta era como sigue:

¿Debe la deducción fiscal por hijo ser mayor para el rico que para el pobre?

Sus alumnos contestaron que no. Era injusto dar mayor ventaja al rico. Ahora veamos el segundo escenario. Supongamos que no existe ninguna deducción fiscal por tener hijos. Pero que en cambio existe una penalización para quien no los tiene. Dicha penalización vendría dada por un impuesto adicional para quien no tenga hijos. Ahora la pregunta es:

¿Debe el pobre sin hijos pagar el mismo impuesto que el rico sin hijos?

De nuevo respondieron que no. Quien tiene más paga más. Es injusto hacer pagar al pobre igual que al rico. Ahora bien, esta situación Schelling explicaba que era contradictoria. Si el que no tiene hijos paga más, es lo mismo que decir que el que tiene hijos paga menos. Esto a su vez nos está diciendo que si queremos que el rico sin hijos pague más impuestos, esto equivale a querer que el rico con hijos tenga una mayor deducción fiscal. Reformular el problema hace que la respuesta cambie por completo.

Enmarcar una propuesta en términos de pérdidas o de ganancias altera la conducta de quien toma la decisión. De igual modo tomar varias decisiones una detrás de otra o una sola que englobe todos los escenarios de golpe también altera el resultado. En el libro se menciona un ejemplo de este artículo del propio Kahneman. En él se preguntaba por cuánto se estaba a dispuesto a pagar para salvar delfines respecto a cuánto se estaba dispuesto a pagar para ayudar trabajadores del campo que padecen cáncer de piel. En el libro nos cuentan que se está más dispuesto a dar más dinero a los delfines, aunque la diferencia no es muy elevada (12.57\$ vs 12.18\$, con elefantes sí que es algo mayor la diferencia). El autor explica que si se presentasen a la vez estas cuestiones nos daríamos cuenta de que en un caso estamos ayudando a una persona y en otro no, por lo que la cifra se revertiría, aunque no aporta evidencia de ello. Sin embargo, de lo que sí aporta evidencia es de las sanciones de las agencias reguladoras estadounidenses. Una multa en materia de seguridad laboral está acotada en 7000 dólares mientras que la Ley de Conservación de Aves Silvestres contempla multas de hasta 25000 dólares. Dentro de cada agencia las sanciones son coherentes entre sí, pero al no haber una puesta en común, los resultados terminan siendo muy dispares. Si hubiese un marco regulatorio común, estos resultados no se observarían.

Teorema de calibración de Mathew Rabin

Este teorema es una continuación de las contradicciones del apartado anterior pero formalizado matemáticamente. Es una prueba de que si rechazas este juego:

50% probabilidad de perder 100€ y 50% probabilidad de ganar 110€.

También deberías rechazar este otro:

50% probabilidad de perder 1000€ y 50% probabilidad de ganar 2.000.000€.

Lo que resulta contradictorio. El teorema se enmarca dentro de la teoría de la utilidad esperada donde las decisiones se toman en base a la esperanza de utilidad y no en función del dinero esperado. Se define una función $U(w)$ que devuelve el valor de la utilidad sobre una cantidad de dinero $w$. Y un maximizador como ellos lo llaman es aquel que se basa en esa función para decidir. Por ejemplo, rechazar la primera apuesta descrita anteriormente se traduce en $0.5 \cdot U(w-100) + 0.5 \cdot U(w+110) < U(w)$. Y aceptar la segunda es equivalente a $0.5 \cdot U(w-1000) + 0.5 \cdot U(w+2.000.000) > U(w)$. Pues la implicación de que aceptar una conlleva aceptar la otra y vice versa no es otra cosa que una descripción de la función de utilidad. En el apartado de la ley de Weber se mostraba que la utilidad del dinero es una función cóncava. Esto nos viene a decir que si trazas una recta sobre dos puntos en la curva, esta quedará por debajo de la propia función. Y esa es la hipótesis final que faltaba para rematar el teorema que dice como sigue:

Quien quiera ver la demostración original puede dirigirse al artículo original. Pero no está muy pulida. Por ejemplo, la hipótesis de $0.5 \cdot U(w-l) + 0.5 \cdot U(w+g) < U(w)$ es innecesaria en la demostración. La propiedad descrita del teorema es válida para toda función cóncava. Una demostración algo más pulida con un análisis más riguroso de las hipótesis se halla en este artículo más moderno. De este teorema tan enrevesado se deduce un colorario que es el que se ha usado para justificar los escenarios del principio:

Aquí es donde realmente sí que se usa la hipótesis de que $0.5 \cdot U(w-l) + 0.5 \cdot U(w+g) < U(w)$. Cabe decir que en la demostración de este corolario se asume que $[w_1, w_2] = \mathbb{R}$, es decir, que de las dos ramas de la función por partes del teorema solo se usa la rama de arriba la cual simplifica los cálculos. Traducido esto significa que la negativa a aceptar o rechazar los juegos propuestos al principio es irrelevante de la fortuna inicial. El propio Rabin reconoce este hecho y dice que incluso si el comportamiento del jugador varía en función de la fortuna inicial, se pueden llegar a conclusiones similares pero requiere de más operaciones algebraicas todavía y el resultado es algo menos fuerte. Para terminar de ejemplificar este corolario veámos qué sucedía en el primer juego. Rechazarlo significaba que $0.5 \cdot U(w-100) + 0.5 \cdot U(w+110) < U(w)$, por lo tanto con este corolario si tomamos $k=5$ nos queda que $1 - \left( 1 - \frac{l}{g} \right) 2 \sum_{i=1}^{k} \left( \frac{g}{l} \right)^i \approx -0.22 < 0$ por tanto $m$ puede ser cualquier valor quedando que $0.5 \cdot U(w-1000) + 0.5 \cdot U(w+2\cdot 10^6) < U(w)$, o lo que es lo mismo, que rechazaríamos jugar aunque el premio fuera de dos millones de euros.

Valores decisorios

La asimetría entre la búsqueda del riesgo en las pérdidas y la aversión al riesgo en las ganancias se extiende un poco más en un patrón de cuatro opciones:

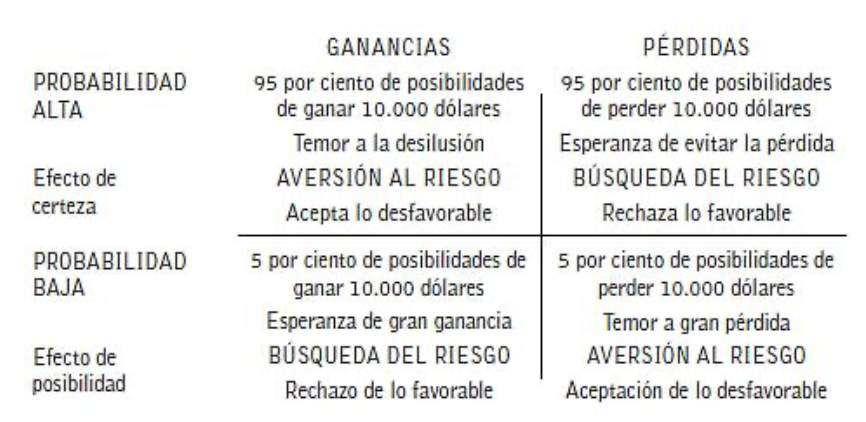
En un intento por explicar esta situación y además resolver la problemática del teorema anterior, Amos y Kahneman hacen una modificación a la función de utilidad añadiendo una función de ponderación de probabilidades. Esta función ha ido evolucionando con el tiempo. El concepto es sencillo, si tienes dos opciones eliges la que tiene mayor valor. Pero calcular ese valor es complicado. En el modelo más básico los agentes racionales simplemente eligen la opción que repercute más ganancias y menos pérdidas, es decir, siguiendo la notación anterior eliges la opción donde $w$ es mayor ($V=w$). Tras analizar que los eventos tienen probabilidades se mide el valor esperado de la ganancia y no la ganancia per se, o sea,

Cuando se consigue entender que el valor monetario no corresponde con el valor real se añade una función de utilidad que es la $U(w)$ y el valor real pasa a ser

Y finalmente, para parchear las incongruencias que resultan del comportamiento humano se añaden ponderaciones a las probabilidades obteniendo la formulación de la teoría de perspectivas:

Es difícil hacer más flexible el marco teórico. Y en concreto cabe preguntarse si $\pi(x) = x$ o no, porque de ser así es una complicación innecesaria. Eso es lo que hicieron Amos y Kahneman en su artículo sobre esta teoría. Para estimar las ponderaciones preguntaron a los participantes sobre qué decisiones tomarían. Siendo las decisiones como esta:

• 50% de probabilidad de ganar 1000€ y 50% probabilidad de no ganar nada.
• 100% de probabilidad de ganar 450€.

Variando las cuantías monetarias y las probabilidades de este tipo de preguntas se puede estimar la función de ponderación $\pi(\cdot)$ de los participantes. El resultado lo presenta en la tabla 4 del capítulo 29.

Quedando palpado el hecho de que $\pi(x) \neq x$. En la traducción al español llaman a esta función de ponderación el valor decisorio. Traducción que no considero muy acertada dada la connotación de la propia formulación. Es cierto que es un valor decisorio porque el experimento utiliza el valor a partir del cual prefieres la opción segura a la opción azarosa. Sin embargo, si se mira desde los ojos del marco teórico esa tabla tiene más sentido si se habla de ponderaciones. En cualquier caso, lo que el estudio de estos valores muestra es que las personas no ponderan las probabilidades de forma lineal. Un incremento del $2\%$ de la probabilidad tiene mucho más peso si es del $98\%$ al $100\%$ que si es del $61\%$ al $63\%$.

Efecto ancla

Este efecto queda ilustrado y medido con el siguiente experimento. En él se les preguntó a los participantes una de estas dos cuestiones:

• ¿Es la altura de la secuoya más alta mayor o menor de 1.200 pies?
• ¿Cuál es su estimación de la altura de la secuoya más alta?

El valor inicial que se da en la pregunta es lo que denominan ancla. Los valores de las preguntas previas eran 844 y 282 respectivamente. Como se puede observar, la presencia del ancla mueve la media en dirección del valor inicial mencionado en la pregunta. Esto es el efecto ancla, que hace que las estimaciones estén condicionadas por el primer valor que se escucha. Y el índice de anclaje es el ratio entre la diferencia de las medias y la diferencia de la media sin ancla y el ancla. O sea, en el caso anterior sería $(844 - 282) / (1200 - 282) = 0.55$, un cincuenta y cinco por ciento.

Este efecto afecta a todos los mortales. Los expertos tasadores inmobiliarios y los jueces no son excepciones. En otro estudio se vio que el índice de anclaje de los tasadores era del 41%. Sus tasaciones se veían afectadas por cifras que los investigadores les habían dado momentos antes de visitar las viviendas. El grupo de control que no tenía conocimientos inmobiliarios sufría un anclaje del 48%, ligeramente superior. Y más sorprendente es el índice de anclaje de los jueces. Un estudio con jueces alemanes mostró que su índice de anclaje era del 50%. En ese experimento a los jueces se les hacía tirar un dado antes de evaluar las condenas. Los dados estaban trucados para que salieran 3 o 9. El resultado fue que los jueces a los que le salía un 9 tendían a dar condenas más altas que aquellos que el dado les marcaba un 3. Este no es el único condicionante mencionado en el libro que afecta a los jueces. En otro capítulo Kahneman nos cuenta como los jueces israelíes tendían a negar la condicional a los reclusos que las solicitaban si el momento de evaluar el informe se daba próximo a la hora de comer. En ese experimento los jueces no sabían que les estaban estudiando.

Ley de los pequeños números

Ese es el nombre que Kahneman le dio a la ignorancia del tamaño muestral a la hora de sacar conclusiones. En muestras pequeñas es posible encontrar resultados sorprendentes debido a la varianza del proceso. Para obtener una conclusión certera uno debe asegurarse de tener una muestra grande para que no quede lugar a dudas. En ese capítulo me llamaron la atención dos ejemplos de esta ley. El primero es el hecho de que los condados con menor tasa de cáncer renal son rurales. La vida en el pueblo es más sana se podría concluir. Pero también es un hecho que los condados con mayor tasa de cáncer renal también son rurales. Debido a que estos condados tienen menor población, la tasa de cáncer renal sufre una mayor varianza. Esto hace que sean los pueblos pequeños los que destaquen con estadísticas muy grandes y también muy pequeñas por puro azar. El segundo ejemplo es más llamativo porque costó 1700 millones de dólares a la fundación Gates. Querían averiguar qué colegios eran mejores y llegaron a la conclusión de que los más pequeños. Lo que los llevó a promover la creación de escuelas más pequeñas. Lo más probable es que sus resultados se debieran precisamente a ley de los pequeños números.

Efecto de dotación

Este efecto se ilustra con el ejemplo de un artículo de Alan B. Krueger. En él se habla de cómo los encuestados no estarían dispuestos a pagar 3000\$ por una entrada de la super bowl porque es muy cara pero a su vez no venderían una entrada por menos de 3000\$. El efecto de dotación es el término usado para referirse a la diferencia entre los precios de compra y venta de los usuarios cuando se trata de bienes de uso vs bienes de intercambio. En las transacciones habituales se vende un objeto que costó 20€ por esa misma cantidad. Pero cuando el poseedor del producto le asocia un valor emocional, el precio de venta y el de compra difieren. El alcance de este efecto y las formas de hacerlo desaparecer aún están por estudiar comenta Kahneman.

La explicación que da Kahneman de este efecto de dotación se basa en la asimetría de las ganancias y las pérdidas. Perder 1€ duele más de la alegría que da ganarlo, como se veían en las gráficas previas de la función de utilidad. Esto hace que se genere esa asimetría de los precios de compra y venta. Esta misma aversión a la pérdida se estudió en el entorno matrimonial quedando registrado que el éxito a largo plazo depende más de evitar lo negativo que de perseguir lo positivo.

Felicidad

Hacia el final del libro se trata sobre varios resultados referentes al estudio de la felicidad. La metodología tiene sus puntos débiles, y considero que esos puntos débiles quedan bastante bien plasmados en este post reciente de Maxim Lott. Aún así son resultados interesantes los que se presentan en el libro. El más remarcable es que la felicidad crece con los ingresos pero se estanca en 75000 dólares al año. Hay múltiples fuentes de este dato, en el libro se basan en este artículo de 2010 realizado por el propio Kahneman. Cuando veo este resultado siempre pienso que me gustaría que hubiese resultados similares en España. El índice de bienestar Gallup-Healthways que es el que se mide en ese estudio solo involucra estadounidenses. Eso hace que sea muy difícil interpretar el resultado. Porque 75000 dólares en Estados Unidos y en 2010 no tienen un equivalente sencillo de calcular en la España de 2024.

Otro hallazgo curioso es que el sufrimiento se distribuye de forma poco uniforme. En el artículo titulado “La mayor parte de la gente es feliz” nos cuentan que en general la gente no experimenta episodios desagradables salvo una minoría que sufre por todos los demás. El resultado se remonta a 1996, mucho antes de las redes sociales y la globalización, por lo que es posible que ya no sea tan aplicable.

Y el último resultado que presento en esta entrada del blog es la gráfica de satisfacción en la vida antes y después del matrimonio

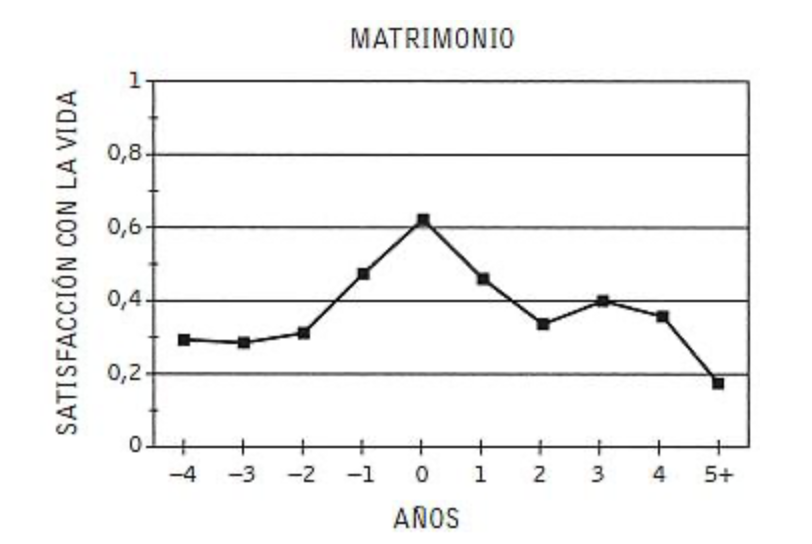
Dejo al lector o lectora que la interprete como quiera.

Conclusión

El objetivo del autor con este libro es proporcionar nuevo vocabulario a sus lectores para sus charletas frente a la maquinilla del café, al mismo tiempo que intenta informar a la sociedad de los sesgos cognitivos que todos padecemos. Es la obra de toda una vida dedicada a la investigación pero desprovista de formalismos y en un lenguaje bastante accesible. Evidentemente el autor tiene sus opiniones y su visión es claramente parcial, algo que él mismo reconoce en el libro cuando habla de una de sus rivalidades con sus adversarios intelectuales. Pero los experimentos son los que son y los datos son datos, no opiniones. Cada cual ha de formarse su propia opinión en base a esos datos con calma y sin prisas. Para mí al principio mi reacción a todos estos resultados no era otra que pensar que el ser humano es imbécil y cabezota. Tras reflexionar debidamente finalmente he concluido que la conducta humana es mucho más compleja de lo que parece. Nuestras experiencias nos forman intuiciones del mundo que habitamos que con frecuencia no son completamente acertadas. Nuestra capacidad ejecutiva se ve afectada por factores externos que raras veces controlamos y tener conocimiento de ello no resuelve el problema. Las apariencias engañan y es muy difícil ser plenamente objetivo y racional. No obstante, cada día se sabe más y se descubren nuevas herramientas para amortiguar el impacto de los sesgos cognitivos. La sociedad evoluciona lentamente, pero lo hace en la dirección correcta.

Extra

Este experimento no es del libro, lo cual es imposible porque es de hace pocos años, pero me llamó mucho la atención. Yo lo conocí por este tweet. En él se dice a los participantes que giren una ruleta en su cabeza que tienen un $20\%$ de probabilidad de salir amarillo y un $80\%$ de salir rojo. Después se hace una encuesta preguntando a la gente que de qué color ha salido la ruleta al girar en su cabeza. El resultado de la encuesta es que alrededor del $80\%$ dijeron que salía rojo y alrededor del $20\%$ dijeron que salía amarillo. Otras personas han reproducido el mismo resultado con otros porcentajes y otras redes sociales y los porcentajes de la encuesta suelen estar en un margen del $5\%$ respecto a las probabilidades imaginarias. Curioso, ¿verdad?